Serpentyna to ćwiczenie, z którym prędzej czy później będzie musiał zmierzyć się jeździec, który nie ustaje w rozwijaniu swoich umiejętności. Jeżeli nie jesteś pewien, jak wykonać serpentynę o 6 zakrętach, skorzystaj z czworobokowej matematyki!
Jak wykonać serpentynę o 6 zakrętach?
Serpentyna to ćwiczenie o dużej wartości gimnastycznej, dlatego często pojawia się w szkoleniu jeźdźca oraz konia. Działa ono zbierająco oraz rozluźniająco. Figura ta zawsze zaczyna się oraz kończy na środku krótkiej ściany, a więc wykonywana jest pomiędzy punktami A oraz C. Po drodze wykonuje się zakręty od jednej długiej ściany ujeżdżalni do drugiej. W gruncie rzeczy są to równo rozłożone półkola połączone liniami prostymi. Liczba wykonywanych zakrętów zależy od poziomu wyszkolenia konia lub jeźdźca.
Być może brzmi to prosto, ale żeby faktycznie uzyskać na czworoboku poprawną serpentynę, należy pamiętać o pewnych zasadach jej wykonywania. W ich zrozumieniu i zapamiętaniu oraz wykonaniu idealnego rysunku przyda się nam na pewno “czworobokowa matematyka”, a wcześniej warto poświęcić także odpowiednią ilość czasu na opanowanie dobrej jazdy na łukach oraz prawidłowego wyjeżdżania kół i wolt.
Jeźdźcy o niższym stopniu zaawansowania mogą ćwiczyć najpierw na wężyku, a potem na serpentynach o mniejszej liczbie zakrętów (2, 3, 4). Jeżeli jednak jesteś już gotowy do przejścia na poziom wyżej, możesz zainteresować się serpentyną o 6 zakrętach. Można ją wykonać na dużym czworoboku, tj. o wymiarach 20×60 metrów.
Ruszamy w punkcie A lub C. Warto pamiętać, że poprzedzający narożnik wyjeżdżamy prawidłowo głęboko. Nie wolno go ścinać, tak jak robimy to jadąc kolejny, czyli pierwszy łuk serpentyny. Warto przyjrzeć się poniższemu rysunkowi, żeby zrozumieć, których punktów na czworoboku musimy szukać po każdym zakręcie. Dobrym punktem odniesienia podczas jazdy może być też dla nas linia od E do B, dzieląca duży czworobok na pół. To właśnie na niej musimy się znaleźć po wykonaniu trzeciego zakrętu.
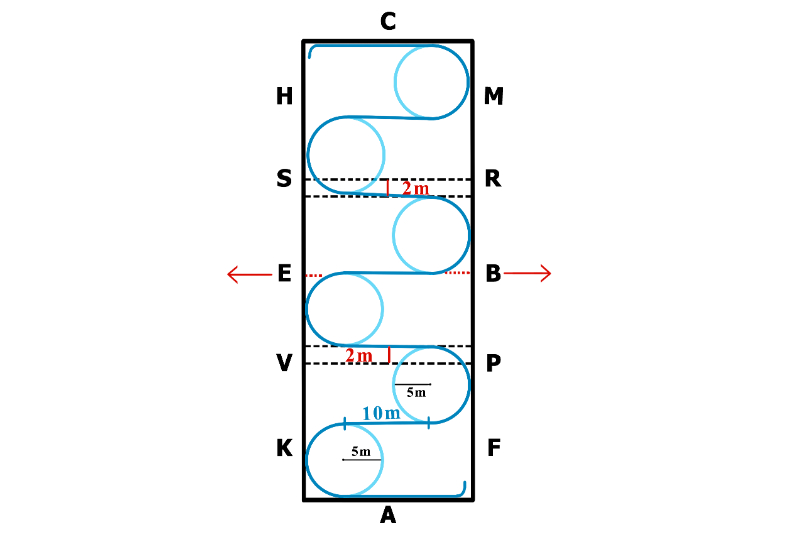
Rys. 1. Serpentyna o 6 zakrętach, rys. Monika Żurek
Żeby wykonać taką serpentynę, musimy sobie wyobrazić sześć wolt o średnicy 10 metrów, rozmieszczonych równolegle po obu stronach czworoboku. Jeśli natomiast będziemy jechać serpentynę o trzech zakrętach, będą to trzy 20-metrowe koła, a jeśli serpentynę o czterech – cztery 15-metrowe.
Po pierwszym „półkółku” mamy przed sobą 10 metrów linii prostej, która prowadzi nas do kolejnego łuku. Zauważ, że im mniejsza jest liczba zakrętów w serpentynie, tym odcinek prostej między łukami będzie krótszy, ponieważ dłużej jedziemy po kole. Zadaniem dla ciebie jest obliczenie, gdzie wypadnie zetknięcie się naszych łuków ze ścianą.
Ważną informacją, która ułatwi poprawne pojechanie serpentyny, jest zasada, że wszystkie serpentyny o parzystej liczbie łuków (czyli 2, 4 lub 6) jedziemy w pewnym momencie przez odcinek X, a te o nieparzystej (3 lub 5 zakrętów – rys. 2) musimy pojechać „zahaczając” o boczną literę E lub B.
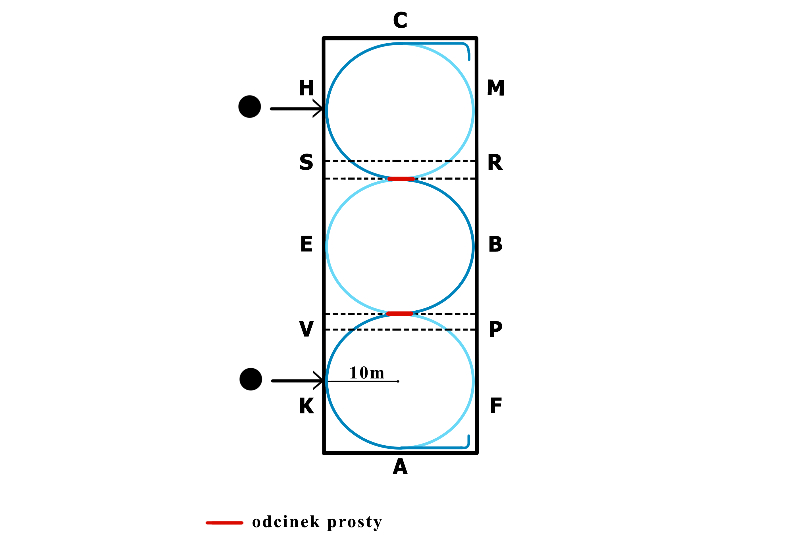
Rys. 2 Serpentyna o 3 zakrętach, rys. Monika Żurek
Opisane powyżej rady to tylko część “matematyki czworobokowej”, ale ten sposób patrzenia na figury ułatwia precyzyjne poruszanie się w szrankach. Polecamy rozrysowywanie sobie każdego elementu przejazdu na kartce w kratkę, zachowując przy tym zasadę, że 1 cm=10 m. Zobaczysz dzięki temu, jak dziwnie wąski i długi jest nasz czworobok.
Tekst powstał we współpracy z Dorotą Urbańską









